La trajectoire suivie :
Les courbes obtenues :
Grâce au GPS et au datalogging nous avons des mesures précises et
régulières à exploiter.
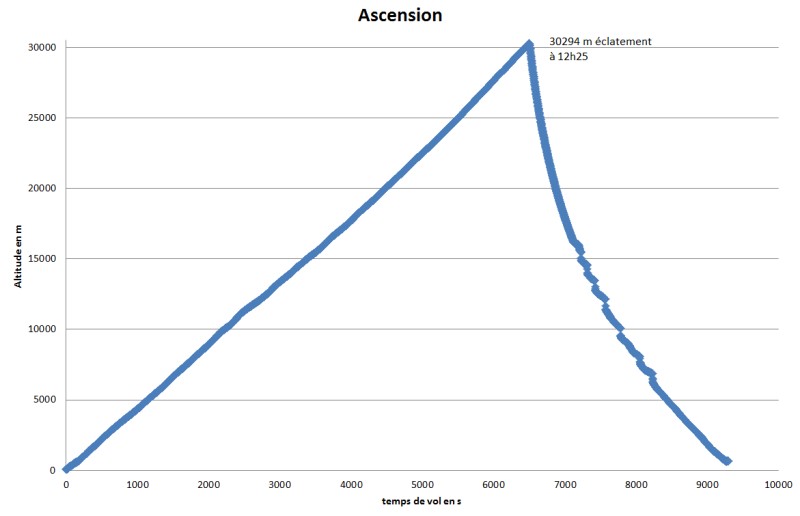
Comme nous l'a annoncé notre aérotechnicien Jean Claude Desarnaud, la vitesse ascencionnelle est constante.
La vitesse ascensionnelle est la pente de la droite, elle vaut 4,6 m.s-1
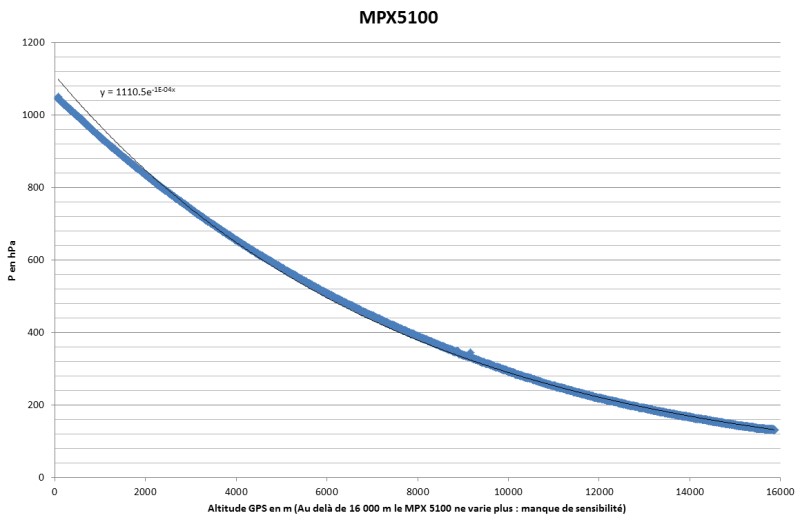
La courbe de pression est elle aussi proche de l'étude théorique menée dans cet exercice de physique : Etude de la pression en fonction de l'altitude, équilibre polytropique de l'atmosphère, ascension d'un ballon
Cette étude donne pour équation : P = P0 e(-1.19.10-4*h)
(pour une atmosphère en équilibre isotherme à 15 °C : c'est le point
faible de ce modèle car T varie...)
Cependant la modélisation de notre courbe nous donne un résultat assez proche :
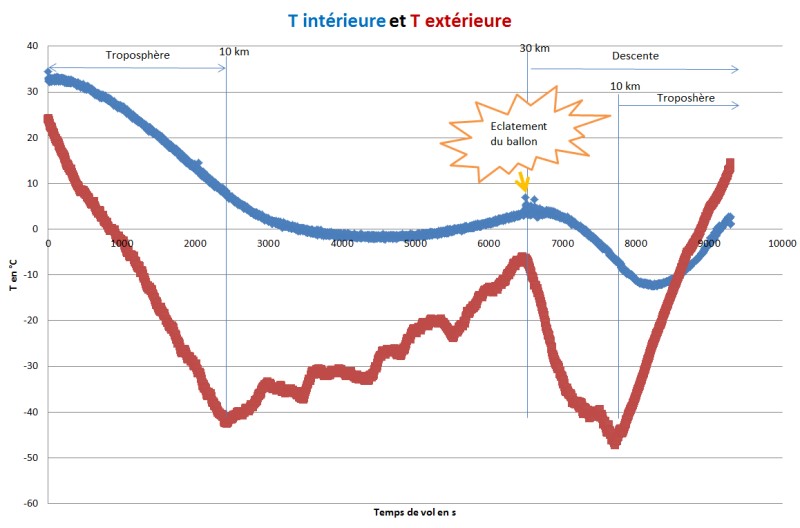
Là aussi les résultats sont conformes à notre attente
:

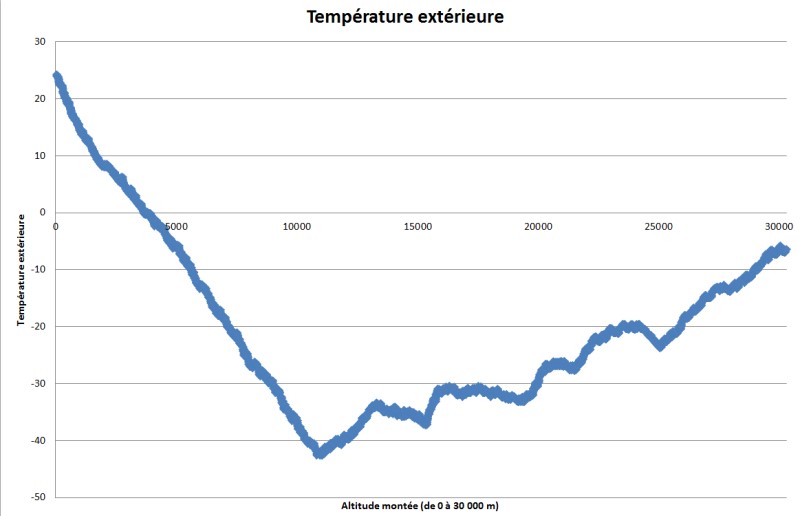
-
le minimum de température (-41 °C) est atteint en haut de la troposphère (10 km)
-
puis la température remonte dans la stratosphère (cliquez sur le schéma...)
-
Pour reprendre l'exercice cité au dessus :
Le modèle de l'atmosphère en équilibre isotherme n'étant pas réaliste, on suppose désormais que dans la troposhpère ( jusqu'à une altitude de 10 km), la température de l'air varie avec l'altitude sous la forme : T(z) = T0(1-kz) où k est une constante positive.
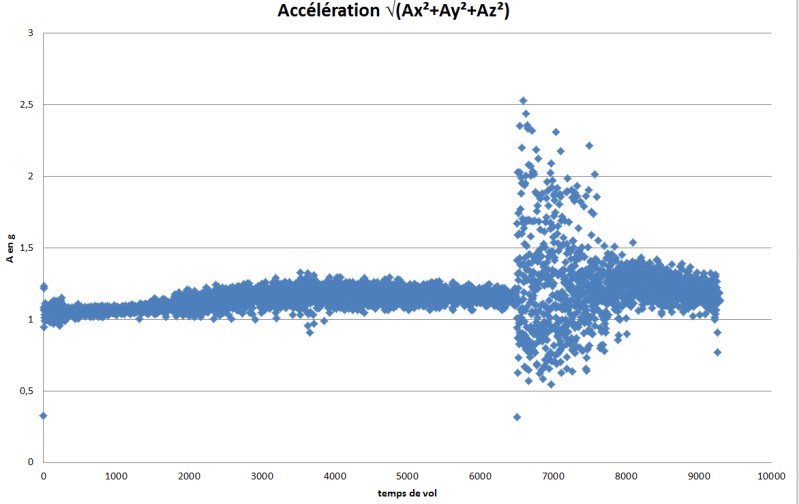
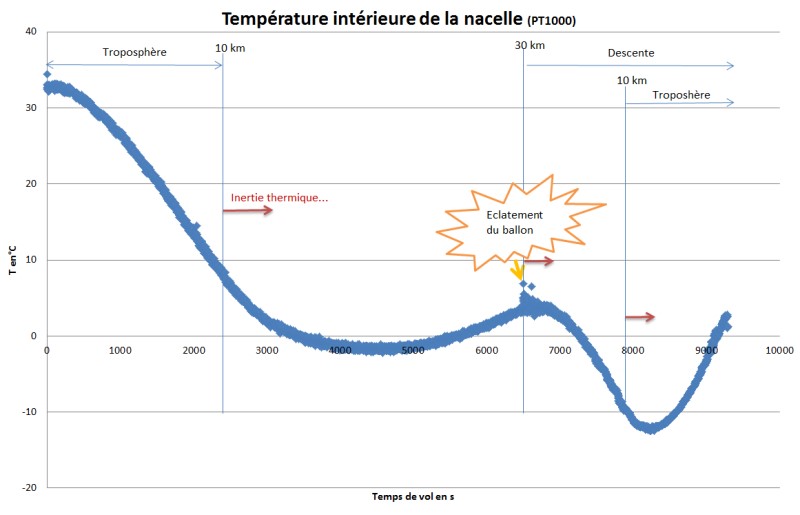
L'accèléromètre détecte bien l'éclatement du ballon et la chute libre qui suit est très mouvementée...